4819. Максимум
по минимуму
Дан ориентированный
невзвешенный граф. Найти в нем вершину, кратчайшее расстояние от которой до
заданной максимально, и вывести это расстояние.
Вход.
В первой строке содержится три натуральных числа n, m и s (1 ≤ s ≤ n ≤ 5000, 1 ≤ m ≤ 20000) – количество вершин и рёбер в графе и номер заданной вершины соответственно. Далее в m строках перечислены рёбра графа. Каждое ребро задаётся парой чисел –
номерами начальной и конечной вершин соответственно.
Выход.
Выведите искомое кратчайшее расстояние.
|
Пример входа 1 |
Пример выхода 1 |
|
3 5 3 1 2 2 1 3 1 2 3 3 3 |
2 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
5 4 5 1 2 2 3 3 4 4 5 |
4 |
РЕШЕНИЕ
поиск в
ширину
Анализ алгоритма
Построим
обратный ориентированный граф – ориентируем каждое ребро в противоположную
сторону. При помощи поиска в ширину найдем кратчайшие расстояния от вершины s. Вершина v, для которой dist[v] максимально, будет искомой. В задаче требуется вывести
значение dist[v].
Пример
Приведенные в
примере графы имеют вид (возле графа слева приведен инвертированный справа
граф):
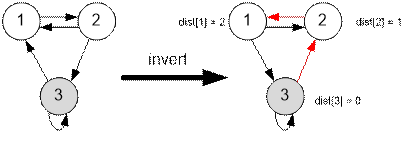
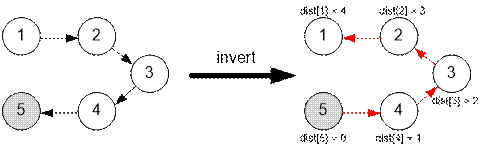
Реализация алгоритма
Объявим матрицу смежности g и массив кратчайших расстояний dist.
#define MAX 5001
int dist[MAX], g[MAX][MAX];
Поиск в ширину из вершины start.
void bfs(int start)
{
Инициализируем массив кратчайших расстояний.
memset(dist, -1, sizeof(dist));
dist[start] = 0;
Объявляем очередь. Заносим в очередь начальную вершину start.
queue<int> q;
q.push(start);
while (!q.empty())
{
int v = q.front(); q.pop();
for (int to = 1; to <= n; to++)
{
if (g[v][to] == 1 && dist[to] ==
-1)
{
q.push(to);
dist[to] = dist[v] + 1;
}
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d", &n, &m, &s);
for (i = 0; i < m; i++)
{
scanf("%d %d", &u,
&v);
Строим граф. Для каждого входного ориентированного ребра u → v занесем в граф обратое v → u.
g[v][u] = 1;
}
Запускаем поиск в ширину из вершины s.
bfs(s);
Находим вершину i с максимальным
расстоянием dist[i].
res = 0;
for (i = 1; i <= n; i++)
if (dist[i] >
res) res = dist[i];
Выводим искомое расстояние.
printf("%d\n", res);